728x90
반응형

📜 문제 내용

🤔 과정
- fibo[n] = fibo[n - 1] + fibo[n - 2] 를 이용한다.
✨ 최초 제출 답안 - ⏱️ 시간 초과
class Solution {
public static int fibo(int n){
if(n <= 1) return n;
return fibo(n - 1) + fibo(n - 2);
}
public int solution(int n) {
int answer = fibo(n);
return answer;
}
}
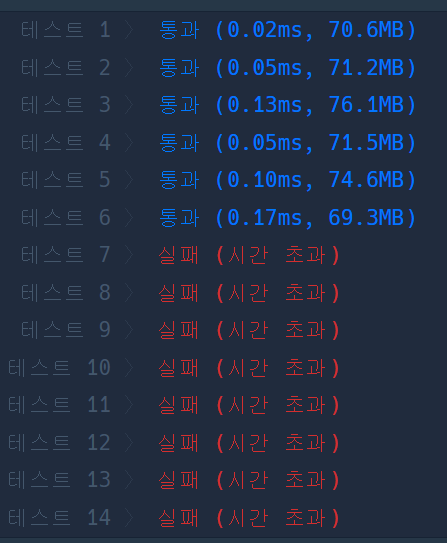
- "피보나치 수" 라는 문제명만 보고 바로 작성했는데, 테스크케이스 14개 중 6개만 맞았다. 문제를 다시 읽어보니, n이 최대 10만 이므로 피보나치 수는 20,899자리 수로 너무 큰 값이며, 문제에서 원하는 값은 n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴해야했다. 그래서 코드를 수정했다.
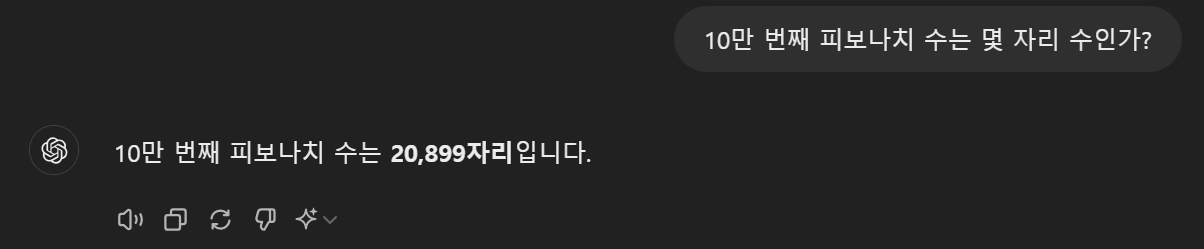
✍️ 재제출 답안
class Solution {
public int solution(int n) {
int[] fibo = new int[n + 1];
fibo[1] = 1;
for(int i = 2; i < fibo.length; i++){
fibo[i] = (fibo[i - 1] + fibo[i - 2]) % 1234567;
}
int answer = fibo[n];
return answer;
}
}
- 마지막에 int answer = fibo[n] % 1234567; 으로 하지 않아도 되는 이유는 다음과 같다.
1) 모듈러 연산의 특징으로 fibo 배열에 넣을 때부터 1234567로 나눈 나머지만을 넣어도 값은 동일하다.
2) 마지막에만 1234567로 나눈 나머지를 처리하면 일단 fibo 배열에 int 자료형을 초과한 너무 큰 값들이 들어간다.
모듈러 연산의 특성
1. (a + b) % m = ((a % m) + (b % m)) % m
2. (a − b) % m = ((a % m) − (b % m) + m) % m
3. (a × b) % m = ((a % m) × (b % m)) % m
- 위의 모듈러 연산 특성 1번으로 인해 마지막에 1234567로 나눈 나머지 처리를 해주는 것과 fibo 자체에 나머지 처리한 값을 미리 넣는 것과 동일하게 된다.
(fibo[n - 1] + fibo[n - 2]) % 1234567 = ((fibo[n - 1] % 1234567) + (fibo[n - 2] % 1234567)) % 1234567
🔗 문제 링크
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
728x90
반응형
728x90
반응형

📜 문제 내용

🤔 과정
- fibo[n] = fibo[n - 1] + fibo[n - 2] 를 이용한다.
✨ 최초 제출 답안 - ⏱️ 시간 초과
class Solution {
public static int fibo(int n){
if(n <= 1) return n;
return fibo(n - 1) + fibo(n - 2);
}
public int solution(int n) {
int answer = fibo(n);
return answer;
}
}

- "피보나치 수" 라는 문제명만 보고 바로 작성했는데, 테스크케이스 14개 중 6개만 맞았다. 문제를 다시 읽어보니, n이 최대 10만 이므로 피보나치 수는 20,899자리 수로 너무 큰 값이며, 문제에서 원하는 값은 n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴해야했다. 그래서 코드를 수정했다.

✍️ 재제출 답안
class Solution {
public int solution(int n) {
int[] fibo = new int[n + 1];
fibo[1] = 1;
for(int i = 2; i < fibo.length; i++){
fibo[i] = (fibo[i - 1] + fibo[i - 2]) % 1234567;
}
int answer = fibo[n];
return answer;
}
}
- 마지막에 int answer = fibo[n] % 1234567; 으로 하지 않아도 되는 이유는 다음과 같다.
1) 모듈러 연산의 특징으로 fibo 배열에 넣을 때부터 1234567로 나눈 나머지만을 넣어도 값은 동일하다.
2) 마지막에만 1234567로 나눈 나머지를 처리하면 일단 fibo 배열에 int 자료형을 초과한 너무 큰 값들이 들어간다.
모듈러 연산의 특성
1. (a + b) % m = ((a % m) + (b % m)) % m
2. (a − b) % m = ((a % m) − (b % m) + m) % m
3. (a × b) % m = ((a % m) × (b % m)) % m
- 위의 모듈러 연산 특성 1번으로 인해 마지막에 1234567로 나눈 나머지 처리를 해주는 것과 fibo 자체에 나머지 처리한 값을 미리 넣는 것과 동일하게 된다.
(fibo[n - 1] + fibo[n - 2]) % 1234567 = ((fibo[n - 1] % 1234567) + (fibo[n - 2] % 1234567)) % 1234567
🔗 문제 링크
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
728x90
반응형
